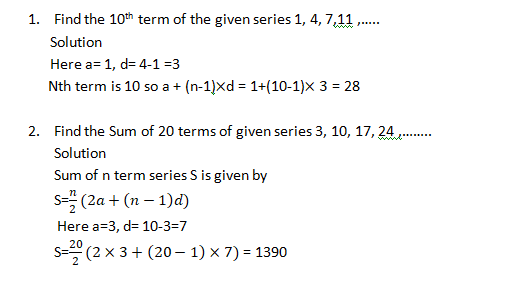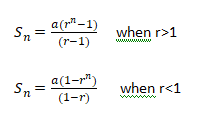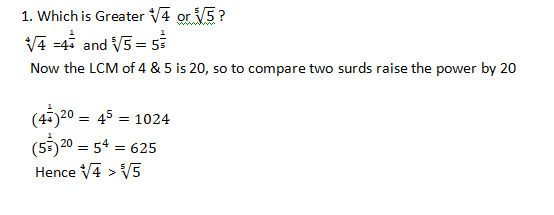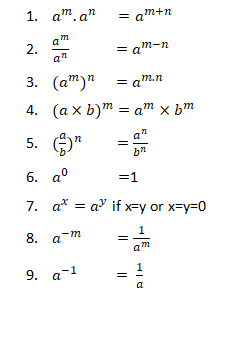Progressions

Most of the questions are asked in Public Sector, Banking and Various Management Entrance Exams.

There are 3 types of Progressions

1. Arithmetic Progression

2. Geometric Progression

3. Harmonic  Progression

Arithmetic Progression 

Quantities are said to be in A.P when they increase or decrease by a common difference.

Example-

1.All Natural Numbers are in A.P with Common Difference 1

   i.e- 1, 2,3,4,5.....

2. All Even and Odd Numbers are in A.P having Common Difference 2

   i.e- even numbers 2,4,6,8...

          odd numbers 1,3,5,7,9....

Arithmetic Progression can be represented as 

a, a+d, a+2.d, a+3.d,........ 

where a- first term

           d- common difference

Nth term of Series 

Sum of Series-

 

To find the Arithmetic Mean between any two given quantities is given by 

Examples

Geometric Progression

Quantities are said to be in G.P when they increase or decrease by constant factor, which is called common ratio.

Example

3, 6, 12, 24, ....

2, 6,18, 54, .....

Geometric Progression can be represented as

nth Term of GP is 

Sum of n term of a G.P

To find Geometric Mean between 2 numbers a, b is given by 

Examples

Harmonic Progression

If a,b,c,d are in Arithmetic Progression then 

Harmonic Mean of a and b is 

Example

All the Three Progressions are discussed and examples are solved for each Progression.

                                                              Thank-You!

Surds, Indices and Logarithms.

A Surd is defined as an Irrational Number.

Laws of Surds

                          

Examples

An Index or Indices is defined as power of the number

Laws of Indices

Example

The Logarithm of any number of a given base is equal to the index to which the base should be raised to obtain the given number.

Properties of Logarithms

                          

Example

Thus the Properties of Surds, Indices and Logarithms are discussed along with an example.

                                                                     Thank-You!

Time and Work and Shortcuts

In Real life we come across practical problems of accomplishing the given project in prescribed time limit. Since the efficiency of different person is different, thus proper note have to be taken.

THEORY 

Let a person A can finish a task in x days and person B finish in y days , then

A can finish 1/x part of work in one day and

B can finish 1/y part of work in one day.

If both work together to finish the task then they can finish as  in one day and days together

Considering in Cases. 

Case 1. Working together

Example 1-

A can finish task in 8 days and B can finish the same in 10 days. How many days are required to finish the task if both are working together.

Solution

A does work in 8 days and thus in one day 1/8 parts

B does work in 10 days and thus in one day 1/10 parts

total work done together in one day is 1/8+1/10 = 9/40 parts

thus 40/9 days needed to do work together i.e. 4 days 4 hrs.

Case 2. Working in Alternate Days

Example 2

Let A can finish the task in 8 days and B can finish the same in 10 days. How many days are required if both are working in alternate days.

Case 2.a- Consider Work Starting from A

Solution

A does work in 8 days and thus in one day 1/8 parts

B does work in 10 days and thus in one day 1/10 parts

Since both are working alternately starting from A , then first 2 days work would be 1/8+1/10 parts, i.e 1st Day A finish 1/8 part and 2nd Day B finish 1/10 part = 8+10/80 =18/80  -----> eqn (1)

From eqn(1) we can tell that total parts of work is 80 .

They both continued to work till 8th day i.e 72/80 parts of work is done , and still 8/80 parts of work is left.

which is to be finished by A on 9th day so, to finish 1/10 part A needs 1/10/1/8 = 4/5

So together they can finish work in 8 days 1 Hr and 20 Minutes.

Case 2.b- Consider Work Starting from B

Solution

A does work in 8 days and thus in one day 1/8 parts

B does work in 10 days and thus in one day 1/10 parts

Since both are working alternately starting from B ,then first 2 days work would be 1/10+1/8 parts, i.e 1st Day A finish 1/8 part and 2nd Day B finish 1/10 part = 10+8/80 =18/80  -----> eqn (1)

From eqn(1) we can tell that total parts of work is 80 .

They both continued to work till 8th day i.e 72/80 parts of work is done , and still 8/80 parts of work is left.

which is to be finished by B on 9th day so, to finish 1/10 part A needs 1/10/1/10 = 1 day

So together they can finish work in 8+1 days = 9 days.

Case 3. Concept of Man , Day, Hour

These are few concepts of Time and Work.

                                                                      Thank-You!

Squares of Numbers and Shortcuts to Find Squares.

Square of Numbers are frequently used for calculation.

The first 30 squares are as follows

Shortcut for Calculation of Squares 

 1. Between 31 to 40

 The Number 60 is taken from twice of 30 and calculated

In the same process squares of the remaining numbers between 31 to 40 can be calculated

2. Between 41 to 50

In the same process squares of the remaining numbers between 41 to 50 can be calculated

3. Between 51 to 60
  
It is same as the above process done for 41 to 50. There we subtracted the digit from 25 and took the value. Here we have to add the value. Process to calculate

In the same process squares of the remaining numbers between 51 to 60 can be calculated.

4.Between 61 to 70

Same as the process used to calculate between 31 to 40. The number 120 is taken as twice of 60

In the same process squares of the remaining numbers between 61 to 70 can be calculated.

5. Between 71 to 80

 Same as 61 to 70. The number 140 is taken from twice of 70

In the same process squares of the remaining numbers between 71 to 80 can be calculated.

6. Between 81 to 90

Same as 71 to 80. The number 160 is taken from twice of 80

In the same process squares of the remaining numbers between 81 to 90 can be calculated

7. Between 91 to 99

Same as 81 to 90. The number 180 is taken from twice of 90

In the similar process squares of the remaining numbers between 91 to 99 can be calculated.

.NOTE - Even the values between 41 to 50 and 51 to 60 can be calculated using technique that has been used to calculate squares between 31 to 40, 61 to 70, 71 to 80, 81 to 90, 91 to 99.
                                                           
Thus the Shortcuts to calculate the squares up-to 100 is discussed.

                                                                         Thank-You!

Remainder Theorem and Polynomial Theorem

As per the Suggestions given- My previous blogs are uploaded with hand written content, from this blog essential things are uploaded as images with content typed in M.S.Word.

Remainder Theorem

Polynomial Theorem

 It is used to find the remainder.

                                                                       Thank-You!

Algebraic Formulae

Some of the Important Algebraic Formulae

Condition of Divisibility for Algebraic Function.

Thank-you!

NUMBER SYSTEM

Hello Friends, This is my Blog. In my blog I would like to share few concepts regarding Aptitude and Reasoning. Which is one of the important scoring concept of today's Competitive Examinations starting from SSC ,BANK PO/ CLERKS, RAILWAYS etc.

The 1st Concept is About NUMBER SYSTEM.

Types of Numbers 

1. Natural Numbers-

                Counting from 1, 2, 3,4 ..... etc are Natural Numbers.

2. Whole Numbers-

                Counting from 0, 1, 2, 3..... etc are Whole Numbers.

3. Integers- 

                Counting from ........-3, -2, -1, 0, 1, 2 ,3,.... are Integers i.e. -infinity to +infinity

                Positive Integers are from  1, 2, 3,.... and Negative Integers are from -1, -2, -3.....

4. Rational Numbers-

                The Numbers of the form P/Q, where P & Q are integers and Q not equal to 0.

                 e.g- 2/3, -4/9 etc

5. Irrational Numbers-

                The Numbers which are not in the form of P/Q or expressed in neither terminating nor                          repeating decimals are known as Irrational Numbers.

                  e.g- π, √3 etc

6. Real Numbers-

                 The Rational and Irrational Numbers combined together are called Real Numbers.

7.Complex Numbers-

                 These can be represented in the form of a+ib. where a and b are real numbers and i=√-1

8. Even Numbers-

                 These are the Numbers which can exactly divisible by 2.

9. Odd Numbers-

                 These are the Numbers which are exactly not divisible by 2.

10. Prime Numbers-

                 These are the Numbers which are divisible b 1 and itself.

11. Composite Numbers-

                  Two Numbers which are greater than 1 and which are not prime numbers.

                  e.g- 4, 6, 9 etc

12. Co-Prime Numbers-

                   Two Numbers which have only 1 as the common factors are called Co-Primes

                    e.g- (3,4), (8,9) etc

TEST FOR DIVISIBILITY

In this Concept we learn how can we identify which number is divisible by which number

1.Divisible by 2

                   A Number is said to be Divisible by 2 if the Unit Digit is Zero or Divisible by 2.

                   e.g- 22, 680, etc

2.Divisible by 3

                   A Number is said to be Divisible by 3, if the sum of the digits is divisible by 3.

                   e.g-2652 etc

                          2+6+5+2= 15 i.e divisible by 3 hence 2652 is divisible by 3

3.Divisible by 4

                   A Number is said to be Divisible by  4 if its last two digits are divisible by 4.

                   e.g- 584 etc

                          84 is divisible by 4 and answer is 21, hence 584 is divisible by 4

4.Divisible by 5-

                  A Number is said to be divisible by 5 if its Unit digit is either 0 or 5.

                  e.g- 1005, 955 etc

5. Divisible by 6-

                  A Number is said to be divisible by 6 if the Sum of Digits is divisible by 3 and is also                           EVEN.

                    e.g- 8448

                            the number is even and 8+4+4+8= 24 which is divisible by 3. Hence 8448 is                                          divisible by 6.

6.Divisible by 8-

                    A Number is said to be divisible by 8 if its last 3 digits is divisible by 8.

                    e.g-  47472 i.e.472 is divisible by 8 and answer 59, thus 47472 is divisible by 8.

7. Divisible by 9-

                    A Number is said to be divisible by 9 if sum of digits is divisible by 9.

8. Divisible by 10-

                    A Number is said to be divisible by 10 if its unit digit is 0.

9. Divisible by 11- 

                     A Number is said to be divisible by 11 if the difference of sum of digit at odd places and                       sum of digits at even places is either 0 or divisible by 11.

                    e.g 1331, even place number 3 and 1 and odd place numbers 1 and 3 so (1+3)-(1+3) = 0

                          thus 1331 is divisible by 11.

H.C.F & L.C.M of Numbers

• H.C.F is Highest Common Factor of two or more numbers is the greatest number that divides each    one of them exactly. It is also called Greatest Common Divisor (G.C.D)
• L.C.M is Least Common Multiple of two or more numbers is the least or lowest number which is exactly divisible by each of them.

Counting of Number of ZERO'S

Procedure with example-

For example we have to count the number of zeros at the end of the value 

10! = 10*9*8*7*6*5*4*3*2*1  i.e.  Basically we count number of fives, because multiplication of five by an even number result in 0 at end product. thus in 10! we have 2 fives i.e 5 as a number and 10 written as 2*5 thus there are total 2 zeros at the end result.

 Cyclicity

 It is used to calculation of Unit digits

These are the few concepts of Number systems. If you'll like my concept do like and share.

And keep waiting for more Blogs

Thank-You!